Carnet de classe de l'école au Pied-de-la-Montagne annexe
Bienvenue dans le carnet de classe des élèves de Martin (DGA-TA élèves dyslexiques) de l'école au Pied-de-la-Montagne annexe de la Commission scolaire de Montréal
Posté par Martin
le 19 février 2009
Les dominos: répertoire mémorisé d'addition
Les dominos
Répertoire mémorisé d'addition
Modélisation avec les élèves en classe du jeu avec le matériel
L'enseignant montre aux élèves comment jouer à ce jeu en les faisant participer (jeu ouvert).
L'enseignant forme une équipe de 6 joueurs en s'incluant.
L'enseignant invite les élèves à s'asseoir par terre avec lui en formant un cercle.
L'enseignant distribue également des dominos à chacun des joueurs et place un domino de départ au centre du cercle.
L'enseignant formule la consigne suivante: Vous devez associer une section de l'un de vos dominos à une extrémité de l'un ou l'autre des dominos déjà posés sur le jeu de manière à obtenir la somme de 11.
Les élèves sont invités à tour de rôle à poser un domino et chercher à obtenir cette somme.
Si l'élève ne parvient pas à poser un domino pour obtenir la somme recherchée, il pige un domino. S'il peut jouer, il peut le faire sans quoi, il passera son tour.
Tout au long du jeu, un élève est invité à prendre en note, sur une feuille ou au tableau, toutes les combinaisons trouvées qui permettent d'obtenir la somme de 11. Cette façon de faire permettra de répertorier toutes les combinaison trouvées que les élèves devront représenter dans leur duo-tang des nombres.

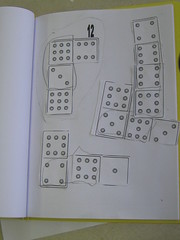
Exemple du duo-tang des nombres (combinaisons qui ont la somme de 12)
 Vidéo du jeu avec les dominos
Vidéo du jeu avec les dominos
Posté par Martin
le 17 février 2009
Activité de l'autobus: sens des opérations

Activité de l'autobus
1) L'enseignant invite un élève à sortir de la classe afin qu'il découvre l'énoncé de la situation qu'il présentera verbalement aux autres élèves.
2) L'enseignant invite les autres élèves à recourir au matériel mis à leur disposition sur une table devant la classe pour se représenter l'énoncé de la situation. On mettra une variété de matériel de manipulation sur la table: bâtonnets, nouilles, jetons, cubes,etc. ainsi que des feuilles de papier brouillon.
3) Un élève est choisi pour représenter l'histoire de l'énoncé au tableau.
4) L'enseignant racontera verbalement l'énoncé de la situation en simulant avec du matériel. L'enseignant aura pris soin de prévoir et d'utiliser pour cette étape un contenant sur lequel sera apposé l'image l'autobus ainsi que des jetons pour représenter les données numériques de l'énoncé.
5) L'élève choisi et les autres élèves sont invités à représenter l'énoncé se la situation avec du matériel.
6) Après avoir raconté l'énoncé, l'enseignant anime une discussion avec les autres élèves et l'élève qui a représenté cet énoncé afin de s'entendre sur la représentation effectuée au tableau. L'enseignant invite les autres élèves à s'assurer si la représentation illustre bien l'énoncé de la situation.
7) Lorsque tous les élèves s'entendent sur la représentation de l'énoncé au tableau, on invite l'élève sorti de la classe à venir afin qu'il puisse raconter l'histoire à partir de ce qui est au tableau.
Benoît Dumas

animation : Martin Gagnon
Posté par Martin
le 29 novembre 2008
Construction d'une collection à partir d'une collection témoin
Présenter rapidement une collection témoin (avec les doigts, cartes à points,dominos) comportant n objets aux élèves. Chaque élève construit une collection avec autant d'objets, n de plus ou n de moins que ceux de la collection témoin.
Qu'as-tu fais pour construire la même collection sur ton bureau? Explique-moi.
*** À ne pas faire*** 
Vous allez voir que sur la vidéo, je montre aux élèves la collection témoin trop longtemps. Je ne veux pas que l'élève compte un à un les objets de la collection témoin. Je veux qu'il se trouve des stratégies pour compter rapidement cette collection.
Posté par Martin
le 26 novembre 2008
Rite de l'appel
L'enseignant invite les élèves à dénombrer le nombre de personnes présentes en classe. L'enseignant touche la tête de chacune des personnes présentes en invitant tous les autres à nommer avec lui un seul mot-nombre pour chaque tête touchée sans oublier de compter parmi les personnes présentes. Lorsque toutes les personnes ont été dénombrées, l'enseignant: aujourd'hui nous sommes n personnes.
Comment je fais pour savoir combien de personnes il y a en classe?
Comment j'ai fait pour bien dénombrer, bien compter?
Comment peux-tu faire pour m'indiquer le nombre de personnes en classe sans avoir à toutes les recompter? Explique-moi
Faire le même exercice avec les personnes qui s'ajoutent dans la classe (intervenants, directeur).
Voici une vidéo tournée en classe:
Il y a plusieurs activités dans ce vidéo. Je vous suggère se commencer par compter avec les élèves. Par après, lorsque les élèves seront habiles avec la chaîne numérique, ils pourront compter eux-mêmes.
Plus tard, les élèves n'auront plus besoin de compter un par un leurs amis. Ils vont le faire mentalement!
Posté par Martin
le 18 novembre 2008
Dénombrer de petites collections réelles ou dessinées
Posté par Martin
le 17 novembre 2008
Dénombrer et comparer de petites collections réelles ou dessinées.
L'enseignant distribue un sac avec des objets. Chaque sac comporte les mêmes objets (ex.: un sac avec seulement des cubes). Prévoir des collections avec le même nombre d'objets (3 sacs de 6 objets, 3 sacs de 7 objets, 3 sacs de 8 objets) dans le but de former plus tard des équipes.
L'enseignant demande à un premier élève combien il a d'objets dans son sac; il demande enseuite à tous ceux qui ont le même nombre d'objets de venir se joindre au premier enfant.
Une fois les équipes formées, les élèves vérifient s'ils ont le même nombre d'objet.
Regardez les élèves en action et découvrez leurs stratégies.
Posté par Martin
le 17 septembre 2008
Séparer une collection en 2 parties égales
Posté par Martin
le 17 septembre 2008
Le dénombrement...trouver la bonne méthode!
Posté par Martin
le 28 avril 2008
multiplication: disposition rectangulaire
Posté par Martin
le 25 avril 2008
Sens des opérations sur des nombes
Posté par Martin
le 24 avril 2008
Opérer sur des nombres plus petits que 1000
Avec cette acivité, je voulais préparer mes élèves à compter une grande collection. J'ai commencé par leur présenter une collection (moins de 300 objets).
1) Les élèves devaient regrouper les objets en paquets de 10.
2) Placer un paquet de 10 dans un petit sac (sac des dizaines).
3) Placer 10 petits sacs dans un moyen sac (sac des centaines).
4) Décrire la collection de différentes façons.
Exemples:
1) J'ai 8 petits sacs, un grand sac et il me reste 2 jetons.
2) J'ai 18 petits sacs et il me reste 2 jetons.
3) J'ai 8 dizaines, une centaine et il me reste 2 jetons.
4) J'ai 18 dizaines et il me reste 2 jetons.
Il n'est pas nécessaire de décrire les collections en respectant l'ordre d'écriture du nombre. le regroupement exprime la valeur et non ps la position.
Voici deux façons de décrire une collection. Je vais en publier d'autres bientôt.
Vous voyez comme il est automatique pour nous de décrire une collectioin en respectant l'odre d'écritures des nombres. Je vais essayer de casser cette mauvaise habitude la prochaine fois! De plus, puisque c'était la première fois, je pose des questions aux élèves. À l'avenir, je vais laisser les élèves parler et moi me taire!!! Il est bon de se filmer et de s'écouter.

Posté par Martin
le 18 avril 2008
Problèmes mathématiques avec de la monnaie
Voici quelques problèmes mathématiques avec de la monnaie.
Puisque mes élèves débutent, j'ai placé des pièces pour les aider. Dans ces problèmes, j'ai placé les pièces que les enfants avaient déjà (Jean a 15 sous). Les élèves devaient compléter pour arriver à la valeur voulue. Voir la photo plus bas.
Sur les photos, il est difficile de voir la réponse des élèves. À l'avenir ils vont l'écrire.
Plus tard, mes élèves vont faire le problème au complet.
Vous pouvez voir les autres photos ici.
Certains élèves ont fait des erreurs. Je voulais les garder, car je vais refaire l'activité. Je voulais aussi garder des traces (portfolio virtuel).
Un gros merci à Anne qui est notre ancienne stagiaire et nouvelle suppléante.
Posté par Martin
le 15 avril 2008
Compter une collection composée de pièces de monnaie
Pour introduire la monnaie, j'ai commencé par faire compter mes élèves par bonds de 5,10 et 25.
Par après, les élèves devaient compter la valeur d'une petite quantité de pièce de monnaie.
Les élèves reçoivent des pièces de monnaie: 10,25,5,10,25
En premier lieu, l'élève doit classer la monnaie de la gauche vers la droite (la première pièce est celle qui a la plus grande valeur 25,25,10,10,5).
Avec trois de mes élèves, je peux me permettre de leur faire compter une collection d'une plus grande valeur.
Après le classement, les élèves peuvent compter la valeur de la collection.
Posté par Martin
le 4 avril 2008
Addition et commutativité
J'ai vécu quelque chose d'assez extraordinaire avec mes élèves dans l'activité que vous allez voir. À chaque année on apprend des nouvelles choses et des nouveaux trucs. Travailler avec des élèves en difficulté est très enrichissant et formateur. Nos élèves participent à notre formation continue!!!
Cette semaine, ma stagiaire a proposé à mes élèves de travailler avec des dominos. Elle voulait travailler les additions. Je n'étais pas capable de rester à ma place et observer. J'ai aussi participé à l'activité.
Par exemple, les élèves devaient trouver toutes les additions qui donnaient 13 comme résultat. Je voulais voir si les élèves allaient trouver une stratégie qui allait leur permettre de sauver du temps pour compter les points. Après quelque essaies, l'équipe des plus petits ont commencé à compter le nombre de point sur le premier dominos et à compléter pour trouver un dominos avec le nombre de points voulu. Ex.: le résultat doit donner 13 et j'ai un dominos de 7. Il comptait sur leur doigt 8-9-10-11-12-13 et il cherchait un dominos à 6 points.
Sur le vidéo, vous aller voir Denalt qui travaille dans l'équipe des grands. Il utilise une autre stratégie que j'ai trouvé intéressante. Puisqu'il ne peut pas compter sur ses doigts (quantité trop grande), il trouve par lui-même une stratégie.
Le but de l'activité n'était pas de leur montrer une stratégie en particulier. Je voulais voir comment ils allaient se débrouiller. Souvent, nos élèves en difficulté doivent se trouver des trucs pour réussir.
L'équipe des petits, ont trouvé que 9+4=13 et que 4+9=13 aussi. Ils étaient heureux parce qu'ils pouvaient trouver 2 fois plus de réponses. J'ai profité de l'occasion pour introduire le concept de commutativité.
J'ai utilisé le jeu avec des dominos à 12 points que l'on peut retrouver dans les grandes surfaces. Il me permet d'aller un peu plus loin que le jeu de 9 points. De plus, on peut l'utiliser plus longtemps avec nos élèves ou nos enfants.
J'ai trouvé des petits jeux sur internet pour compter les points sur un domino (comptage et comparaison).
Posté par Martin
le 31 mars 2008
Dénombrer
Avant de dénombrer, je voulais m'assurer que mes élèves avaient la conservation du nombre. J'ai pris une collections de 15 objets. Les élèves devaient dénombrer à partir de la droite et à partir de la gauche. J'ai déplacé les objets afin de les faire dénombrer à nouveau. Puisque mes élèves ont entre 8 et 10 ans, ils ont la conservation du nombre. Il faut retenir que mes élèves sont dans une classe DGA (un retard de 2 ans en français et en mathématique).
Pour aller plus loin, j'ai donné aux élèves des collections avec plus d'objets. Dans les vidéos que vous allez voir, je voulais faire dénombrer les élèves en leur faisant faire des paquets de 10.
Dans la première vidéo, mes élèves comptent leur collection. J'essaie un peu de les mélanger pour leur faire prendre conscience qu'ils doivent trouver un moyen efficace pour dénombre une collection sans se tromper.
Dans la deuxième vidéo, je demande aux élèves de m'expliquer comment
ils ont procédé pour dénombrer leur collection. Remarquez Denalt qui
regroupe ses objets (groupes de 10).
Posté par Martin
le 6 février 2008
Petit jeu à faire en classe ou à la maison
Voici une activié favorisant le développement des concepts, des processus ou des savoir essentiels en arithmétique
Compter avec la chaîne numérique verbale
Jeu du 7 up
Comment jouer?
Les élèves comptent à partir de 1 et lorsque dans le nombre il y a un 7, l'enfant dit 7 up ou claque des mains. Pour augmenter le niveau de difficulté du jeu, on ajoute 2 nombres. Par exemple, lorsque dans un nombre il y a le chiffre 2 et 5 l'élève dit 7 up ou clague des mains.

- • Mot de bienvenue
- • Plans de la semaine
- • Activité sportive
- • Arts plastiques
- • Danse
- • Des sites à visiter
- • Formation Benoît Dumas Mathématique
- • Formation Isabelle Faucher Français
- • Français
- • Jeunes Naturalistes
- • Le coin de Barbara
- • Les petits mots de Martin
- • Les trucs de Laurence
- • Les trucs de Michelle
- • Mathématique
- • Résoudre une situation-problème
- • Déployer un raisonnement mathématique
- • Communiquer à l'aide du langage mathématique
- • Pojet mathématique
- • art dramatique
- • champions de la dictée
- • cirque
- • code de vie
- • conscience phonologique
- • controle
- • correspondance Québec-Belgique
- • mon dictionnaire personnel
- • règles orthographiques
- • science
- • événements spéciaux
- Dysfonction érectile


sabine sur :
• Addition et commutativité
Martin sur :
• Addition et commutativité
Sabine sur :
• Addition et commutativité
Geneviève Tremblay sur :
• Dénombrer

Les carnets que nous aimons bien visiter





